Infinitas

Lemniscus Iacobi Bernoulli, una ex figuris lemniscatis quae adhibetur ad infinitatem significandam.

Formula:Res (Formula:Pns), $\mathrm{\infty }$ notata, est notio quasi numerica quae adhibetur ad multas sententias mathematicas, philosophicas, et theologicas explicandas, quibus omnibus absentia finium aut termini modis variis intellegitur.

Nonnumquam homines, in locutione vulgari, loquuntur de infinitate in rebus finitis sed diu perennibus; ita hora, si quid invitus facere cogaris, videatur infinita. In aliis talibus casibus, saepe infinitas significat "rem maiorem quam maximam quam excogitari possit". Saepe etiam, homines loquuntur de plure quam infinitas, vel infinitate + 1, quae immo quippe ambae sunt nugae.

In mathematica, infinitas usurpatur quasi numero reali. In quibusdam autem scholis rationis, infinitas e contrario non putatur esse numerus, sed conceptio theoretica.

In philosophia, tempus spatiumque ratione infinitatis explicentur, ut descripsit antinomia prima Immanuelis Kantii. Infinitum tempus appellatur Aeternitas. In philosophia Graeca, gratia exempli in eo quod Anaximander τὸ Ἄπειρον appellavit, infinitas est origo et fons omnium. In rebus theologicis, infinitas fit Deus. In theologia Iudaeo-Christiana, sicut in operibus Ioannes Duns Scoti, notio deitatis est infinitus non quantitate, at potestate.

Ut legas de spatio infinito, vide Universum.

Systemata Numerica Mathematicae

Numeri Elementarii
Naturales $\mathbb{N}$ {0,1,2,3,...} sive {1,2,3,...} Primi $\mathbb{P}$ {2,3,5,7,11,...} Abundantes Amicabiles Compositi Defectivi Perfecti Sociabiles Integri $\mathbb{Z}$ {...,-2,-1,0,+1,+2,...} Pares {...,-2,0,+2,...} Impares {...,-3,-1,+1,+3,...} Rationales $\mathbb{Q}$ Reales $ℝ$ Irrationales Numerus pi $\pi =3.14159265358979\dots$ Numerus Euleri $e=2.718281828459045\dots$ Complexi ℂ Algebraici Transcendentes Numerus imaginarius $i=\sqrt{-1}$ Quaterni $ℍ$ Octoni $𝕆$ Infinitas $\mathrm{\infty }$
Variae radices
Radix binaria(2) Radix octalis(8) Radix decimalis(10) Radix sedecimalis(16)

De signo $\mathrm{\infty }$

Iohannes Wallis fuit primus qui lemniscum quasi symbolum infinitatis in litteratura mathematica introduxit.

Imago urobori, qui saepe est pictus in forma lemniscata. De De Lapide Philisophico, a Luca Iennisio.

Origines signi $\mathrm{\infty }$ non clare cognoscuntur. Figura ipsa appellatur lemniscus, et in animo concipi potest modum quo iter trans curvum simplicem a lemnisco factum numquam finiret.

Aequatio Cartesiana quae lemniscum reddit est:

$(x^2+y^2{)}^2=2a^2(x^2-y^2)$

Vulgo fama est $\mathrm{\infty }$ signum derivatum esse a Moebii taenia. Item, in animo potest iter concipi aeternum trans faciem sine finibus. Haec autem explicatio haud sufficit, quoniam $\mathrm{\infty }$ scribebatur ad infinitatem significandam fere ducentos annos prius quam Augustus Ferdinandus Moebius et Iohannes Benedictus Listing invenerint Moebii taeniam anno 1858.

Iohannes Wallis saepissime fertur instituisse $\mathrm{\infty }$ ad infinitatem scribendam anno 1655, in suo libro De sectionibus conicis. Coniectatur hoc signum a numero Romano pro 1000 derivatum esse, ipsum a numero Etrusco pro 1000, quod est specie CIƆ, et interdum significabat Romanis modo "plurima". Propositum etiam derivatum esse a littera Graeca ω (omega), littera ultima abecedarii Graeci.

Etiam symbolum inventum est in arte vulgari, et in symbolis religiosis antiquis. Gratia exempli, οὐροβóρος saepe est pictus in forma lemnisci.

In Unicodice, $\mathrm{\infty }$ designatur a ∞ , codice (U+221E) (∞).

Sententiae de Infinitate per historiam

Per saecula, homines in noctis caelum intuebantur, universi fines coniectantes. Etiam enumerabant de finibus numerorum mirantes. Natura ergo infinitatem vel eius rationem petebant. Textus antiquissimi nobis noti sunt de philosophis Indicis.

Sententiae antiquae Orientales

Yajurveda

Inter primas sententias infinitatis notas reperitur in libro Indico Yajurveda ("scientia precum orationis solutae") c. 1200–900 ante aer. vulg.) qui continet hanc sententiam: "si ex infinitate removeas, vel infinitati addas, infinitas etiam remanet." Verbis exactis Sanscriticis:

Genni

Crux gammata, symbolum Gennorum.

Genni, in opere mathematico Surya Prajnapti (c. 400 ante aer. vulg.) omnibus numeris tres categorias attribuerunt. Quisque categoria ultra divisa est in tribus ordinibus:

• Enumerabiles : minores, medii, maiores.
• Innumerabiles : fere innumerabiles, vere innumerabiles, infinite innumerabiles.
• Infiniti : fere infiniti, vere infiniti, infinite infiniti.

Genni primi fuerunt qui dixerunt omnes infinitates non esse aequas. Infinitates dissimiles agnoverant quattuor, quae sunt: recta infinitas in una dimensione, quadrata infinitas in duabus dimensionibus, cubica infinitas in tribus dimensionibus, et infinita infinitas in dimensionibus infinitis.

Secundum Singh (1987), Joseph (2000), et Agrawal (2000), maximus numerus enumerablis N hominum Ianorum est hodierna aleph-null ${\mathrm{\aleph }}_0$ (numeri cardinalis notio copiae iinfinitae integrorum 1, 2, . . . .), minimi transfiniti numeri cardinalis.

Sententiae priores Europaeae

In Europa, primi Graeci de infinitate finxerunt.

Pythagoras

Pyhtagoras docebat unitatem esse numerum maximae gravitatis; fontem omnium numerorum, ut facile numeremus ad infinitatem, modo unum addentes ad numerum priorem.

Parmenides et Zeno Eleaticus

Paradoxum Zenonis, de Achille et Testudine.

Parmenides docebat praecepta Pythagoreis similia: dixit unum esse omnia, quod unus in partibus infinitis dividi posset.

Zeno Eleaticus diversa paradoxa proposuit ut theorias Parmenidis illustraret (circiter 460 ante aer. vulg.). In uno ex his, quod est servatum et explicatum in Aristotelis Physicis, Achilles cursu Testudinem persequitur, at numquam potest praeterire, quod Achille ad locum Testudinis assecuto, iam Testudo ultra moverit. Ita hoc modo continuant ad infinitum:

Aristoteles

Aristoteles a Francisco Hayez depictus, 1811.

In Europa et scholis rationis Europaeis hodiernis, theoria solita ab Aristotele data est (circa 350 ante aer. vulg.):

Hoc discrimen inter "infinitum potentia" et "infinitum actu" diu magni momenti erat inter philosophos Europaeos. Attamen duae sententiae in loco citato complicantur, quarum altera est numerari semper posse praeter quemlibet numerum, etiamsi tot tantaeve res non existent. Altera est posse quantificare super series infinitas absque impeditione. Exempli gratia, $\mathrm{\forall }n\in \mathbb{Z}(\mathrm{\exists }m\in \mathbb{Z}[m>n\wedge P(m)])$, id est: "dato integro ullo n, est integer m > n ut P(m)".

Archimedes et Plotinus

Archimedes usurpavit infinitatem in eodem modo calculi integralis. Clarissimum exemplum fuit inventio valoris π. Circa 250 ante aer. vulg., et in maxime parte ad sapientiam Eudoxi Cnidii, Archimedes propulsit progressum ad infinitatem intelligendam, rationem limitum investigans. Circumscripsit circum circulum polygonum, cuius latera omnia circuli circumitum tectigit, et scripsit intra circulum polygonum, cuius anguli omnes tectigerunt. Si latera polygonorum augescunt, differentia inter suas areas areae circuli appropinquat. Ubi Archimedes inscribit et circumscribit polygona 96 laterum, approximavit valorem π est inter 3 + 1/7 (~3.1429) et 3 + 10/71 (~3.1408). Ut late noscetur, π est numerus irrationalis, cuius inventio valde Pythagoreanos vexavit. Archimedes scripsit π numeros praeter punctum decimalem infinitos continere, et suam approximationem numquam eius valorem totum advenituram esse. At etiam sciit suam approximationem valori toto approprinquaturam esse, dum latera polygonorum ad infinitatem augescunt. Hoc modo viam struxit ad caclculum cum limitibus.

Ratio Archimedei approximationis π

In alio opere, Archimedes temptavit numerum harenularum quae Universum impleat calculare, rationem quae dicit multitudines maximas infinitam esse dimittens.

Sententiae Mediaevales

Guillelmus de Ockham

Parmenidis Aristotelisque sententias simplicius scripserunt auctores mediaevales, sicut Guillelmus de Ockham (1327):

Ergo, infinitus non potest esse ullus numerus, quod cuilibet numero semper erit numerus maior magnitudine, "quia non tot quin plures."

Sententiae a Renascentia usque ad hodiernum diem

Galilaeus

Galilaeus ab Equite Passignano, circiter annum 1642.

Galilaeus primus notavit biiectionem serierum infinitorum, cum ullis suorum subserierum. Exempli gratia, series numerorum quadratum {1, 4, 9, 16 . . .} coordinetur cum radicibus suis, nempe numeris naturalibus {1, 2, 3, 4 . . .} in hoc modo (1638:

1, 2, 3, 4, . . .

↓  ↓  ↓  ↓

1, 4, 9, 16, . . .

Videbatur ab hac dialectica ut series natura minor (ita, quod modo continet aliquot non omnes numeros seriei) quam serie cuius est pars sit, aliquo modo, eadem magnitudine. Hanc dixit Galilaeus esse "ex istis difficultatibus, quae suam ducunt originem ex discursu quem intellectus noster finitus circa infinita instituit". In dialogis De duabus novis scientiis, Salviati, cum Sagredo Simplicioque in elencho colloquens, dicit haec:

Lockius

Ioannes Lockius, pictus ab Gotfrey KnellerFormula:Dubsig equite, 1697

Ioannes Lockius, sicut philosophi empiristae, homines credidit non posse infinitatem intellegere. Asseruit nostros sensus nobis indicare omnia de mundo quae possimus intellegere, quoniam omnes sensus, et omnia quae possunt sentire sint natura finiti, ergo quippe necessitate nostrae cogitationes esse finitas. Nostra ratio de infinitate esse "negativa" vel "privitiva" (circa 1680):

Sententiae hodiernae

"Duae res tantum sunt infinitae: universum, et stultitia hominum. De priore autem haud sum certus."--Albertus Einstein

Blake

Gulielmus Blake a Thomas Phillips pictus (1807).

Gulielmus Blake autem credidit nostram inopiam perceptionis esse impeditionem primam in infinitatem intelligendam. Dixit (1793):

Cantor

Georgius Cantor

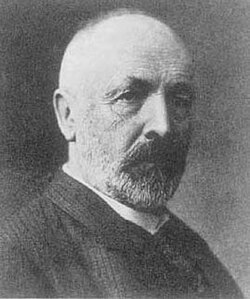
Georgius Cantor biiectionis theoriam Galilaei refellit in suo argumento diagonali (1891):

Per indicem serierum ab 0is et 1is constructorum infinitum, instruamus novam sequentiam elementorum s₀ ut eius elementum primum differat ab elemento primo primae sequentiae in indice, elementum secundum differat ab elemento secundo secundae sequentiae in indice, et cetera in hoc modo, ut n^um elementum diferat ab n^o elemento n^ae sequentiae. Ita, s_0,m erit 0 si s_m,m est 1, et s_0,m erit 1 si s_m,m est 0.

Exempli gratia:

s₁ = (0, 0, 0, 0, 0, 0, 0, ...)

s₂ = (1, 1, 1, 1, 1, 1, 1, ...)

s₃ = (0, 1, 0, 1, 0, 1, 0, ...)

s₄ = (1, 0, 1, 0, 1, 0, 1, ...)

s₅ = (1, 1, 0, 1, 0, 1, 1, ...)

s₆ = (0, 0, 1, 1, 0, 1, 1, ...)

s₇ = (1, 0, 0, 0, 1, 0, 0, ...)

...

s₀ = (1, 0, 1, 1, 1, 0, 1, ...)

(Elementa s_1,1, s_2,2, s_3,3, et cetera litteris fortis scribuntur, ut ratio nominis diagonalis plane videatur.)

Deinde sequitur ut series T, ab infinitis sequentiis zerorum unorumque non poniatur in indicem s₁, s₂, s₃, ... Nisi, in illo modo instruamus sequentiam s₀ qui et sit in indice T (quia est sequentia zerorum unorumque de sequentiis in T natura est ipsa in T), et simul non est in T (quod eam instruamus ut diferat ab omnibus sequentiis in T aliis).

Ergo T non conferatur cum numeris naturalibus a biiectione. Brevius: est innumerabilis.

Wittgenstein

Natura infinitatis etiam disputatur. Aliqui putant esse partem mathematicae, alii philosophiae. Alii ultra ambas coniungunt, sicut Ludovicus Wittgenstein qui impetum saeve egit in theoriam seriei axiomaticam (1933):

Infinitas in mathematica

Via parametrica Moebii taeniae, quae est symbolum infinitatis mathematicum.

Infinitas est numerus maior magnitudine quam omnes numeri naturales vel numeri reales. Est tam magna, ut homines vix possint magnitudinem intellegere. Attamen, sicut cum $\sqrt{-1}$, quae quoque vix intellegitur, infinitas perfacile tractatur in functionibus mathematicis.

Proprietates infinitatis arithmeticae

Infinitas non est numerus purum at tamen consideretur pars esse lineae numerorum realium, in qua arithmetica opera possunt ad infinitatem pertinientes perfaci. Subter sunt multae operationes arithmeticae cum Infinitate et aliis numeris.

$-\mathrm{\infty }$ . . . . . . $+\mathrm{\infty }$

Infinitas secum

1. $\mathrm{\infty }+\mathrm{\infty }=\mathrm{\infty }$, et $-\mathrm{\infty }+(-\mathrm{\infty })=-\mathrm{\infty }$

2. $\mathrm{\infty }\cdot \mathrm{\infty }=x$, et $-\mathrm{\infty }\cdot (-\mathrm{\infty })=x$, et $\mathrm{\infty }\cdot (-\mathrm{\infty })=-x$

Aequationes cum infinitate purisque numeris

1. $-\mathrm{\infty }<x<\mathrm{\infty }$

2. $x+\mathrm{\infty }=\mathrm{\infty }$, et $x+(-\mathrm{\infty })=-\mathrm{\infty }$

3. $x-\mathrm{\infty }=-\mathrm{\infty }$, et $x-(-\mathrm{\infty })=\mathrm{\infty }$

4. $\frac{x}{\mathrm{\infty }}=0$, et $\frac{x}{-\mathrm{\infty }}=0$

5. Si $x>0$ deinde

$x\cdot \mathrm{\infty }=\mathrm{\infty }$

$x\cdot (-\mathrm{\infty })=-\mathrm{\infty }$

6. Quod si $x<0$ deinde

$x\cdot \mathrm{\infty }=-\mathrm{\infty }$

$x\cdot (-\mathrm{\infty })=\mathrm{\infty }$

Operationes indefinitae

1. $0\cdot \mathrm{\infty }$, et $0\cdot (-\mathrm{\infty })$

2. $\mathrm{\infty }+(-\mathrm{\infty })$, et $\mathrm{\infty }-\mathrm{\infty }$

3. $\frac{\pm \mathrm{\infty }}{\pm \mathrm{\infty }}$

4. ${(\pm \mathrm{\infty })}^0$

5. $1^{\pm \mathrm{\infty }}$

6. $\mathrm{\infty }+\mathrm{\infty }=\mathrm{\infty }\cdot \mathrm{\infty }=(-\mathrm{\infty })\cdot (-\mathrm{\infty })=\mathrm{\infty }$

7. $(-\mathrm{\infty })+(-\mathrm{\infty })=\mathrm{\infty }\cdot (-\mathrm{\infty })=(-\mathrm{\infty })\cdot \mathrm{\infty }=-\mathrm{\infty }$

Alia notanda

Nota bene $[\frac{x}{\mathrm{\infty }}=0]\equiv ̸[0\cdot \mathrm{\infty }=x]$. Hoc est quia zero multiplicatur infinitate non definitur.

Nota etiam $[\frac{x}{\mathrm{\infty }}=0]$ non aequare $[0\cdot \mathrm{\infty }=x]$. Si secunda esset vera, necesse sit vera ess pro omni x, et a transitivitate aequalium relationis, omnes numeri sint aequales. Hoc est significantia indefinitatis sententiae $0\cdot \mathrm{\infty }$.

Etiam per Hospitalii regulam, limes solutionum indefinitarum pro aequatione n inveniantur, si aequatio scribatur forma $\frac{\mathrm{\infty }}{\mathrm{\infty }}$ vel $\frac{0}{0}$, quae saepe solutionem definitam producit.

Infinitas in analysi reali et calculus infinitesimalis

In analysi reali, signum $\mathrm{\infty }$, "infinitas" appellatur, denotat limitem infinitam. $x\to \mathrm{\infty }$ significat x crescere ultra quemlibet valorem designatum, et $x\to -\mathrm{\infty }$ significat x tandem aliquando minus fieri quam quilibet valor designatus.

Infinitas saepe adhibetur non solum ad limitem definiendam, immo etiam in analysi reali quasi numerus realis esset; si f(t) ≥ 0 deinde:

• $\underset{0}{\overset{1}{\int }}f(t)dt=\mathrm{\infty }$ significat f(t) non definire aream finitam ab 0 ad 1.
• $\underset{0}{\overset{\mathrm{\infty }}{\int }}f(t)dt=\mathrm{\infty }$ significat aream sub f(t) infinitam esse.
• $\underset{0}{\overset{\mathrm{\infty }}{\int }}f(t)dt=1$ significat aream sub f(t) appropinquere 1

Infinitas in geometria

Partes multarum figurarum geometricarum sunt infinitae. Ex centro circuli inifiniti radii describantur. Linea in duas partes dimidiatas bipartiatur ad infinitum; semper erit etiam linea ex qua duae sectiones extraheatur.

Torricellius

Sinistra pars Torricellii cornu.

Figura ad dextram inventa est anno 1644 ab Evangelista Torricellio, appellatur Torricellii cornu. Eius copia est finita, at area superfaciei est infinita. Torricellii verbis: Formula:Citatio

Simiae infinitae

Simia machina dactylographica utitur.

Est sententia sensu prisca et forma multiplex quae saepius hodie contexitur a simiis infinitis. Breviter, dicit sortes cuiusdam eventus improbabilis, temptatas per vices infinitas, tandem infinitati appropinquaturas. Elegantius, suasum est si esset infinitus simiarum numerus cum digitis forte cadentibus in superfaciem infinitarum machinarum dactylographicarum, statim corpus integrum Gulielmi Shakespeare scriptum fore.

Ut dictum est, huius sensus sententiae priscus est, et Cicero ipse dedit fontem, at re vera dubitans, Ennio loco Shakespeare: Formula:Citatio

Infinitas in fictione scientiae

In The Hitchhiker's Guide to the Galaxy sunt hae definitiones infinitatis: Formula:Citatio2

Nexus interni

• Absolutum (philosophia)
• Aeternitas
• Apiron
• Calculus infinitesimalis
• Fragor Maximus
• Infinitum uno addito

Fontes

Bibliographia

• Formula:Cite book
• Agrawal, D. P. 2000. Ancient Jaina Mathematics: an Introduction. Infinity Foundation.
• Formula:Cite book
• Jain, L. C. 1973. Set theory in the Jaina school of mathematics. Indian Journal of History of Science.
• Formula:Cite book
• O'Connor, John J., et Edmund F. Robertson. 1998. Georg Ferdinand Ludwig Philipp Cantor. MacTutor History of Mathematics archive.
• O'Connor, John J., et Edmund F. Robertson. 2000. Jaina mathematics. MacTutor History of Mathematics archive.
• Pearce, Ian 2002. Jainism. MacTutor History of Mathematics archive.
• Formula:Cite book
• Singh, N. 1988. 'Jaina Theory of Actual Infinity and Transfinite Numbers', Journal of Asiatic Society, Vol. 30.
• Formula:Cite book

Nexus externi

• Numerare ad infinitatem
• Doctulum in mathematica infinitorum, a Peter Suber, de St. John's Review, XLIV, 2 (1998) 1-59.
• Infinity, Principia Cybernetica
• Caupona Infinity
• Sententiae finitatis infinitatisque in philosophia
• Fons medievalium recentumque scriptionum de Infinitate