Lemma zigzag

Lemma zigzag, vel fortasse lemma flexuosum, in mathematica, praecipue in algebra homologica, dicit fieri singularis sequentia longa exacta in gregibus homologicis quorumdam multiplicium catenariorum. Effectus est in omne categoria abeliana validus.

Formula

In categoria abeliana (sicut categoria gregum abelianorum vel categoria spatiorum vectoralium super campum datum), liceat

$(𝒜,{\partial }_{\bullet }),(ℬ,{\partial }_{{\bullet }^{\prime }})$ et $(𝒞,{\partial }_{{\bullet }^{″}})$ esse multiplices catenarumFormula:Dubsig qui ad sequentem sequentiam brevem exactam conveniunt:

$0⟶𝒜\stackrel{\alpha }{⟶}ℬ\stackrel{\beta }{⟶}𝒞⟶0$

Talis sequentia est imminutio huius diagrammatis commutativi:

ubi ordines sunt sequentiae exactae et quaeque columna est multiplex.

Lemma zigzag dicit esse congeries tabularum finium

${\delta }_n:H_n(𝒞)⟶H_{n-1}(𝒜),$

quae sequentem sequentiam exactam efficit:

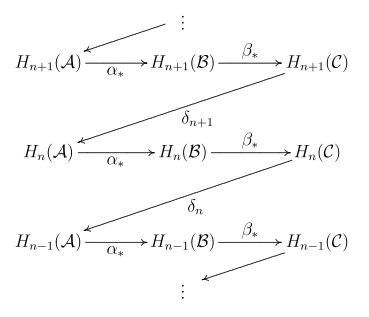
Tabulae ${\alpha }_{*}^{}$ et ${\beta }_{*}^{}$ sunt tabulae ab homologia usitate inductae. Tabulae finium ${\delta }_n^{}$ alibi explicantur. Nomen lemmatis ex moribus "zigzag" tabularum hac in sequentia oritur. Similiter autem hoc theorema etiam lemma vipereum late appellatur, quamquam alius exitus in algebra homologica eiusdem nominis fit. Hoc "aliud" lemma vipereum ad probandum lemma zigzag adhiberi potest.

• Sequentia Mayer–Vietoris

Bibliographia

• Hatcher, Allen. 2002. Algebraic Topology. Cantabrigiae: Cambridge University Press. ISBN 0-521-79540-0. [1].
• Lang, Serge. 2002. Algebra. Graduate Texts in Mathematics, 211. Ed. 3a, retractata. Novi Eboraci: Springer-Verlag. ISBN 978-0-387-95385-4, MR1878556.
• Munkres, James R. 1993. Elements of Algebraic Topology. Novi Eboraci: Westview Press. ISBN 0-201-62728-0.